Hướng dẫn phân tích độ phức tạp thuật toán chi tiết

Độ phức tạp của giải thuật là một cách để đánh giá hiệu quả của một giải thuật dựa trên hai yếu tố chính:
- Độ phức tạp thời gian: Là lượng thời gian cần thiết để giải thuật thực thi, thường được biểu diễn dưới dạng số lần thực hiện các phép toán cơ bản.
- Độ phức tạp không gian: Là lượng bộ nhớ cần thiết để giải thuật hoạt động, bao gồm cả bộ nhớ dành cho biến, cấu trúc dữ liệu và ngăn xếp lời gọi hàm.
Độ phức tạp thường được biểu diễn bằng ký hiệu Big-O (O-notation), miêu tả tốc độ tăng trưởng của thời gian hoặc không gian khi kích thước đầu vào tăng lên.
Các bước tính độ phức tạp của giải thuật
-
Xác định kích thước đầu vào:
- Xác định biến hoặc tham số đầu vào ảnh hưởng đến thời gian chạy (thường được ký hiệu là
n).
- Xác định biến hoặc tham số đầu vào ảnh hưởng đến thời gian chạy (thường được ký hiệu là
-
Xác định số lần thực hiện các phép toán cơ bản:
- Đếm số lần lặp, so sánh, tính toán, hoặc truy cập dữ liệu cần thiết trong giải thuật.
-
Loại bỏ các hằng số và hệ số nhỏ:
- Trong Big-O, chúng ta chỉ quan tâm đến tốc độ tăng trưởng, vì vậy loại bỏ các hằng số hoặc các bậc thấp hơn.
- Ví dụ: nếu số phép tính là 23n2+5n+2, ta chỉ quan tâm đến bậc cao nhất n2n^2n2, vậy độ phức tạp là O(n^2).
-
Tìm trường hợp xấu nhất (Worst Case):
- Đánh giá giải thuật trong trường hợp mất nhiều thời gian nhất (tình huống bất lợi nhất).
Một số ví dụ
-
Giải thuật duyệt mảng:
for (int i = 0; i < n; i++) { Console.WriteLine(arr[i]); }Có một vòng lặp chạy từ 0 đến n−1n-1n−1, vậy độ phức tạp thời gian là O(n)
-
Giải thuật sắp xếp Bubble Sort:
for (int i = 0; i < n - 1; i++) { for (int j = 0; j < n - i - 1; j++) { if (arr[j] > arr[j + 1]) { // Hoán đổi int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } }- Có hai vòng lặp lồng nhau, mỗi vòng chạy tối đa nnn lần, nên tổng thời gian là O(n^2)).
-
Tìm kiếm nhị phân:
while (low <= high) { int mid = (low + high) / 2; if (arr[mid] == target) return mid; else if (arr[mid] < target) low = mid + 1; else high = mid - 1; }- Ở mỗi bước, dải tìm kiếm giảm đi một nửa, vậy độ phức tạp là O(\log n).
Một số mức độ phức tạp thường gặp
- O(1): Thời gian không phụ thuộc vào kích thước đầu vào (ví dụ: truy cập phần tử trong mảng).
- O(\log n): Tăng trưởng logarithmic, thường gặp trong các giải thuật chia để trị (như tìm kiếm nhị phân).
- O(n): Tăng trưởng tuyến tính, phổ biến khi duyệt qua tất cả phần tử của đầu vào.
- O(n \log n): Thường gặp trong các giải thuật sắp xếp hiệu quả như Merge Sort hoặc Quick Sort.
- O(n^2): Tăng trưởng bậc hai, phổ biến trong các giải thuật sử dụng hai vòng lặp lồng nhau (như Bubble Sort).
- O(2^n) hoặc O(n!): Tăng trưởng rất nhanh, thường gặp trong các bài toán đệ quy hoặc tổ hợp phức tạp.
Tác giả: Bạch Ngọc Toàn
Chú ý: Tất cả các bài viết trên TEDU.COM.VN đều thuộc bản quyền TEDU, yêu cầu dẫn nguồn khi trích lại trên website khác.
Tags:
Bài viết liên quan
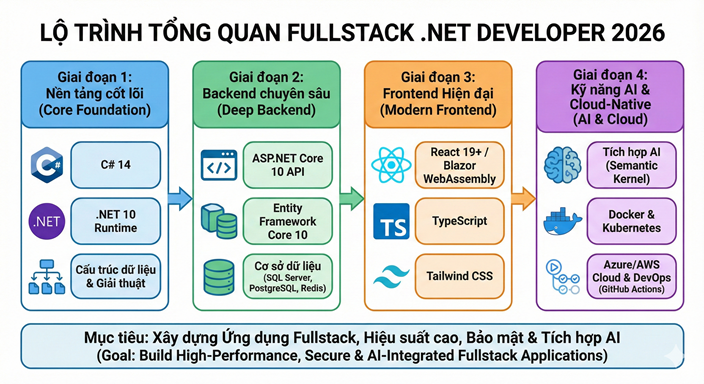
Lộ trình Fullstack .NET Developer 2026
Chào bạn, bước sang năm 2026, lộ trình của một Fullstack .NET Developer đã có những thay đổi quan trọng để thích nghi với sự lên ngôi của AI, điện toán đám mây và phiên bản .NET 10 (LTS) vừa ra mắt cuối năm 2025.
Đọc thêm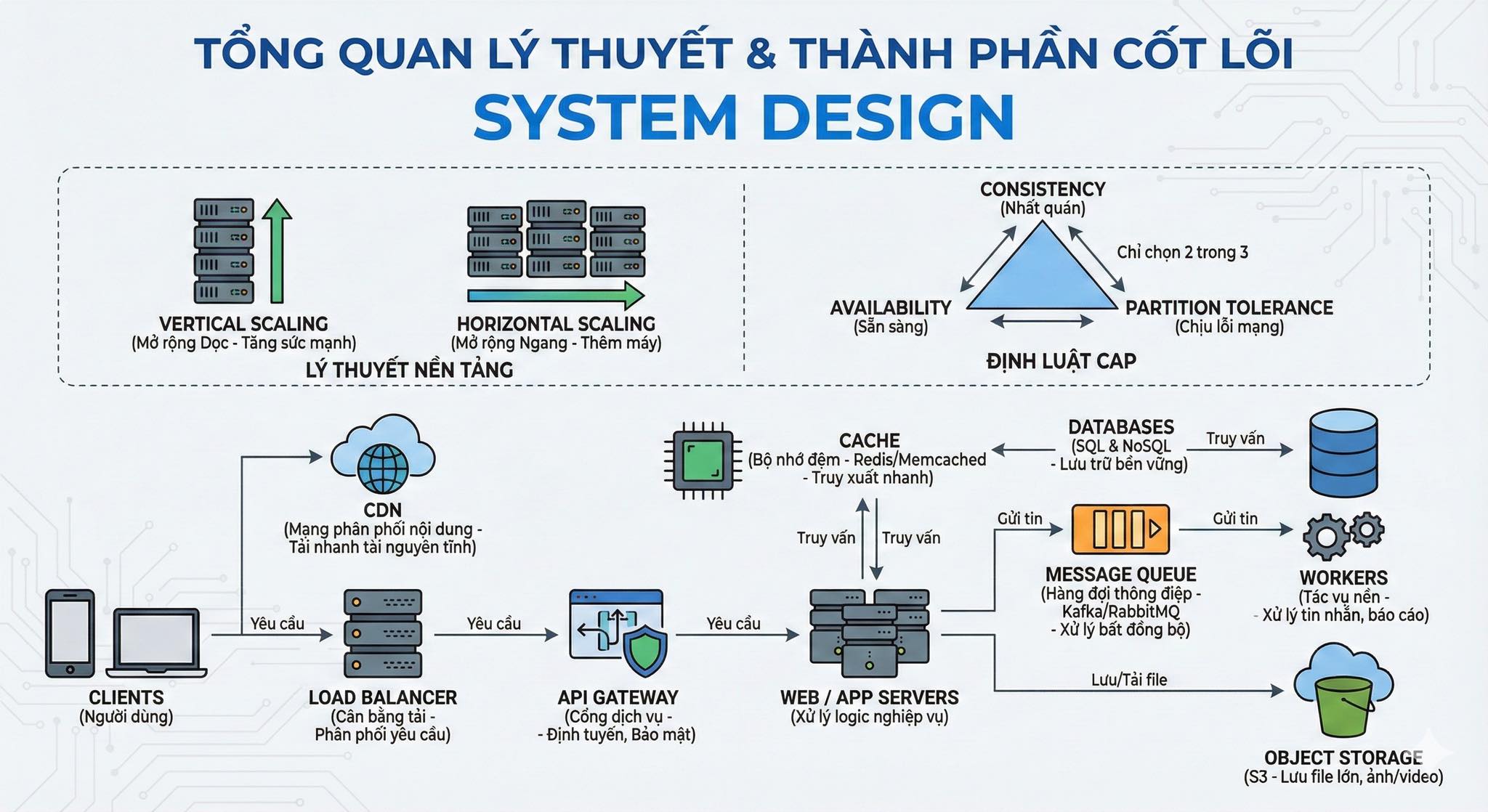
TỔNG QUAN LÝ THUYẾT & THÀNH PHẦN CỐT LÕI SYSTEM DESIGN
Các lý thuyết cốt lõi trong System Design
Đọc thêm
Cẩm nang Big-O: Thước đo hiệu năng thuật toán trong C#
Hiểu rõ Big-O từ O(1) đến O(n!) qua ví dụ C# thuần. Bí quyết tối ưu code, chọn đúng cấu trúc dữ liệu để hệ thống luôn chạy nhanh và ổn định.
Đọc thêm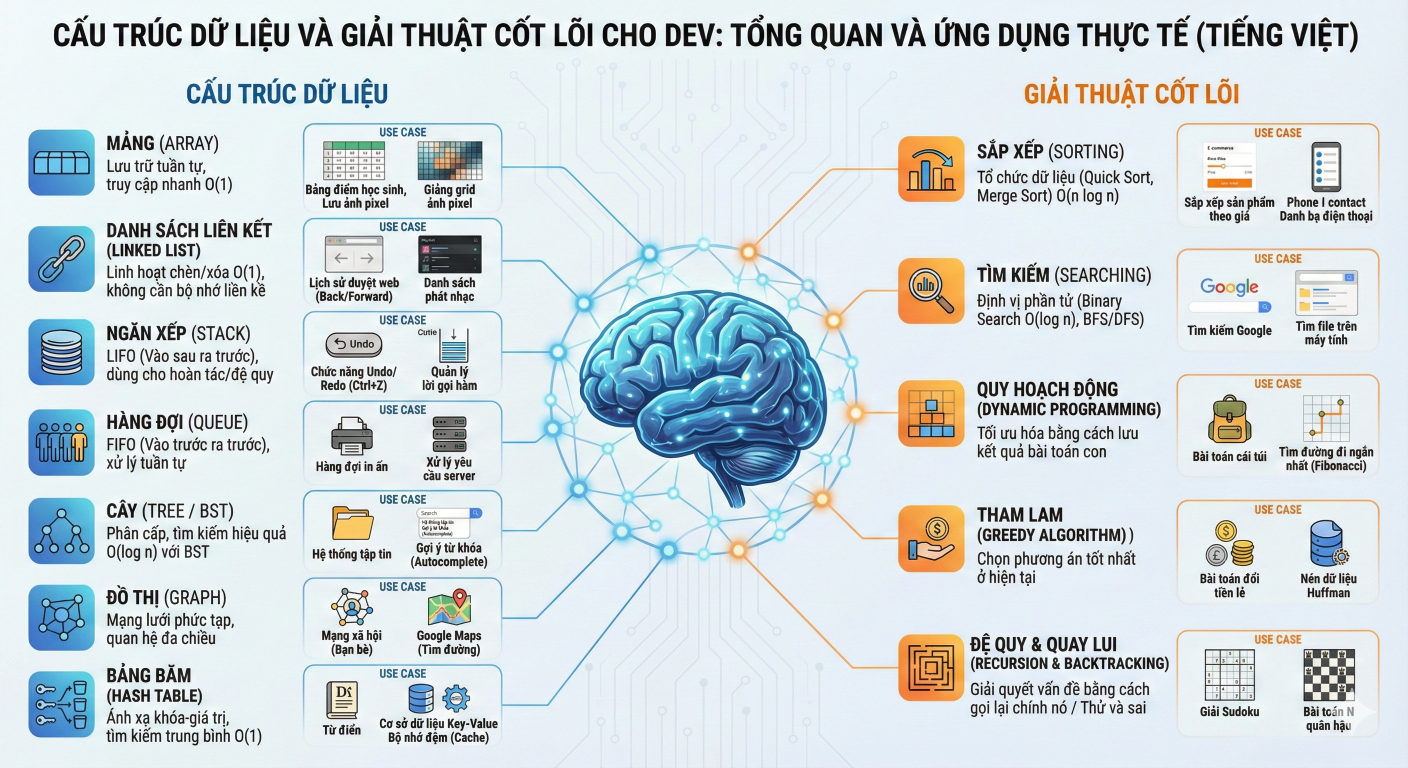
Bản Đồ Tư Duy Cho Dev: Giải Mã Cấu Trúc Dữ Liệu & Giải Thuật Cốt Lõi
Đọc thêm

Các mẫu thiết kế (design patterns) phổ biến trong kiến trúc Microservices.
Các mẫu thiết kế (design patterns) phổ biến trong kiến trúc Microservices.
Đọc thêm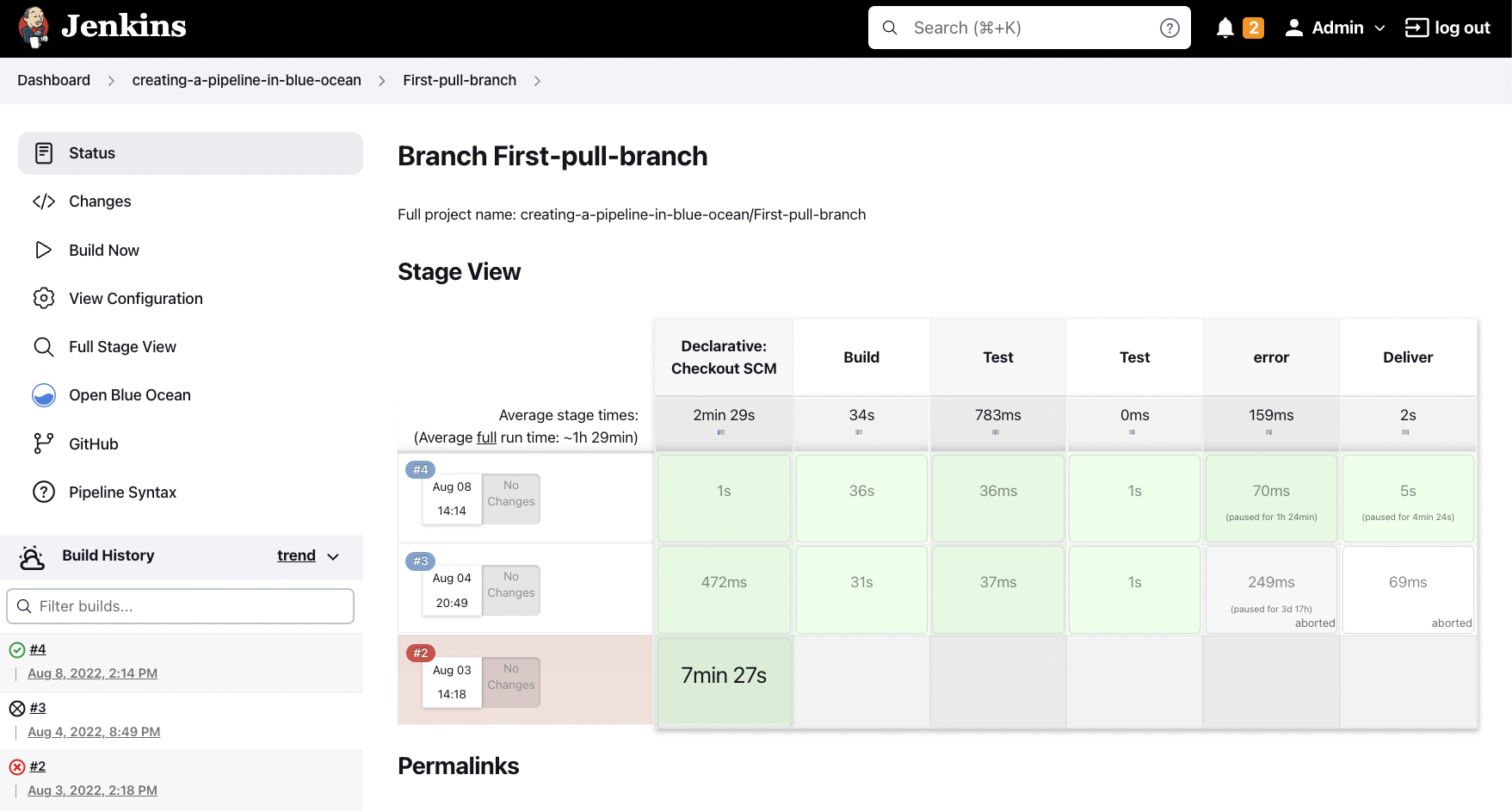
Hướng dẫn Bind Jenkins vào IIS trên Windows bằng Reverse Proxy
Cho phép truy cập Jenkins từ một subdomain (ví dụ jenkins.tedu.com.vn) thay vì phải gõ http://localhost:8080.
Đọc thêm
Hiểu về AI, LLM, RAG và Agentic RAG trong 15 phút
Trong vài năm gần đây, trí tuệ nhân tạo (AI) đã bùng nổ mạnh mẽ và trở thành tâm điểm của cả thế giới công nghệ. Nhưng đi kèm với nó là hàng loạt khái niệm mới như LLM, RAG, hay Agentic RAG khiến nhiều người mới bắt đầu cảm thấy lúng túng.
Đọc thêm
Hướng dẫn tự triển khai N8N trên CentOS bằng Docker Compose và NGINX
N8N là công cụ mã nguồn mở cho phép bạn tự động hóa quy trình làm việc (workflow automation) và tích hợp nhiều dịch vụ khác nhau mà không cần phải lập trình.
Đọc thêm
Bài 6. Các thao tác với XPath và Selector trong Selenium
Bài viết này hướng dẫn bạn làm việc XPath và Css Selector trong Selenium.
Đọc thêm
Bài 5. Các thao tác với Web Browser trong Selenium
Bài viết này hướng dẫn bạn làm việc sâu Web Browser trong Selenium.
Đọc thêm